The BraiNum project aims at developing a mathematical model for the physiological and pathological function of the brain and central nervous system. In this endeavor, we exploit the power and flexibility of mathematical modeling, numerical analysis, and high-performance scientific computing.
BrainNum project is developed at the Laboratory for Modeling and Scientific Computing (MOX) of the Department of Mathematics, Politecnico di Milano.
We focus on:
- Neurodegenerative diseases: high incidence (about 1/1000 subjects worldwide) and have a major clinical and societal impact on national systems. Their investigation and treatment are still the subject of open discussion in the medical community, and their study is ever more relevant, due to the overall aging of the world population.
- Neurological disorders: broad spectrum of pathological conditions related to the impairment of neural firing rate or signal transmission. Epilepsy (the most common) affects 50 million people worldwide, and acute seizures entail possibly severe physical injuries.
Research Team
Paola F. Antonietti
(Principal Investigator)
Collaborators
Mathematical modeling of the brain and CNS
The computational modeling of the Central Nervous System (CNS) entails several challenges:
- anatomic complexity: cerebral gyri and sulci, ventricles, vasculature, and ducti
- multiphysics: electrophysiology, blood supply and perfusion, dynamics of the cerebrospinal fluid (CSF), protein distribution and clearance, long-term remodeling
- multiscale: from single cell (neuron firing, axon mechanical remodeling, …) to the whole organ (signal propagation, blood and CSF dynamics, cerebral tissue poroelasticity, prion clearance, …); from milliseconds (electrical activation) to decades (neurodegeneration and remodeling)
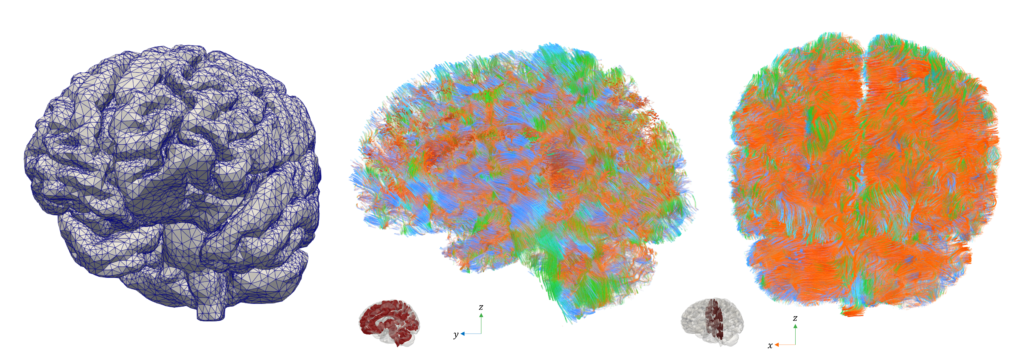
![Arterial pressure, CSF pressure, and tissue displacement resulting from a multiple network poroelasticity simulation in physiological conditions [Corti, Antonietti, Dede’, Quarteroni. M3AS, accepted (2023)]<br />](https://brainum.mox.polimi.it/wp-content/uploads/2023/05/MPETCompartimenti.png "MPETCompartimenti")
Arterial pressure, CSF pressure, and tissue displacement resulting from a multiple network poroelasticity simulation in physiological conditions [Corti, Antonietti, Dede’, Quarteroni. M3AS, accepted (2023)]
![Arterial pressure, CSF pressure, and tissue displacement resulting from a multiple network poroelasticity simulation in physiological conditions [Corti, Antonietti, Dede’, Quarteroni. M3AS, accepted (2023)]<br />](https://www.mate.polimi.it/servizi/biblioteca/quaderni/upload/img/mox-img-20231011185231.png "MPETCompartimenti")
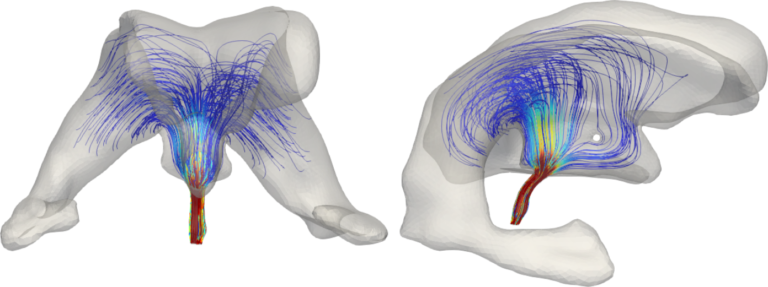
Intracranial pressure and parenchymal displacement obtained simulating the coupling between the CSF in the brain ventricles and the surrounding poroelastic tissue [Fumagalli, Corti, Parolini, Antonietti. arXiv:2310.07651 (2023)]
Neurodegenerative diseases
Modeling of:
- CSF flow: waste clearance and its impairment in neurodegeneration (time scale: seconds/minutes)
- distribution of misfolded proteins (time scale: years)
- neural axon degeneration and brain remodeling (time scale: decades)
- anatomic complexity: cerebral gyri and sulci, ventricles, vasculature, and ducti
- multiphysics: electrophysiology, blood supply and perfusion, dynamics of the cerebrospinal fluid (CSF), protein distribution and clearance, long-term remodeling
- multiscale: from single cell (neuron firing, axon mechanical remodeling, …) to the whole organ (signal propagation, blood and CSF dynamics, cerebral tissue poroelasticity, prion clearance, …); from milliseconds (electrical activation) to decades (neurodegeneration and remodeling)
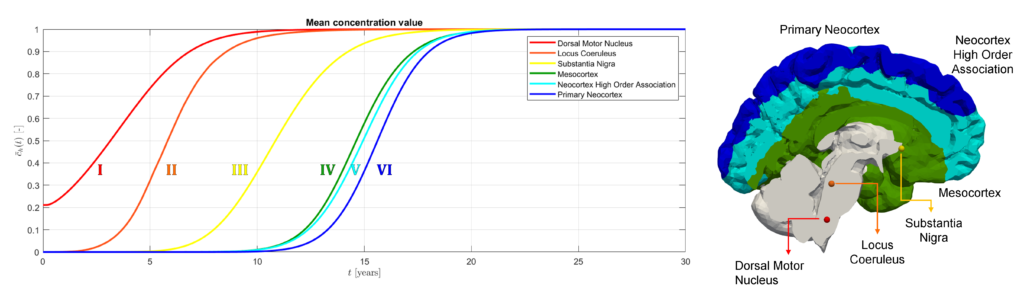
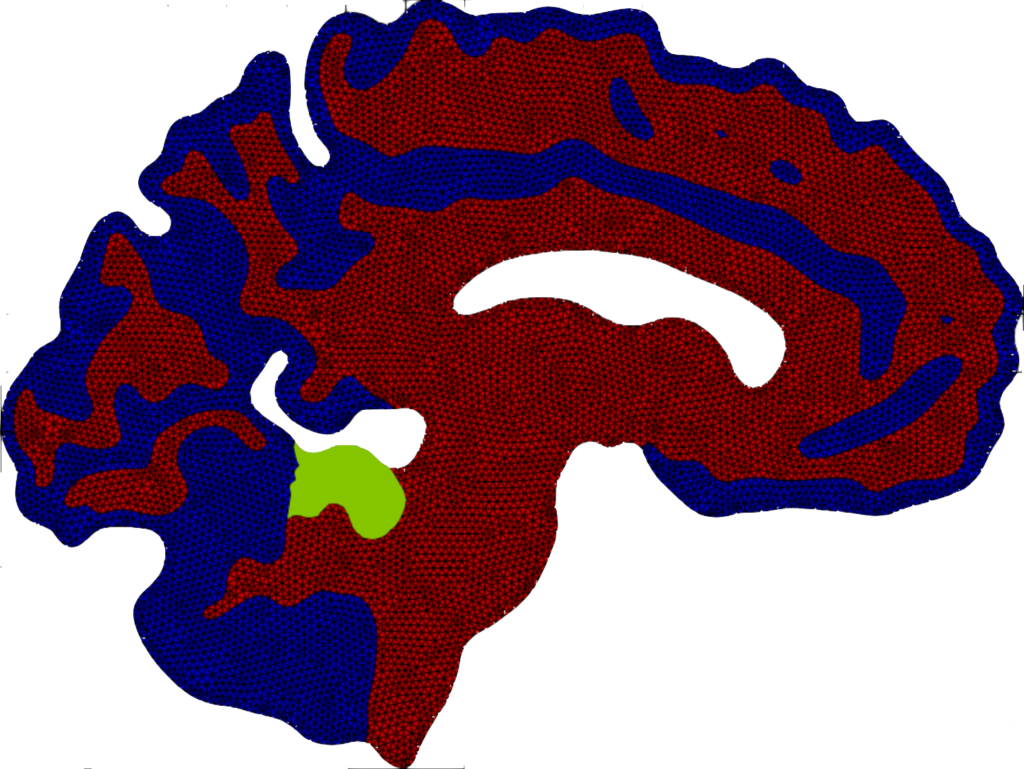
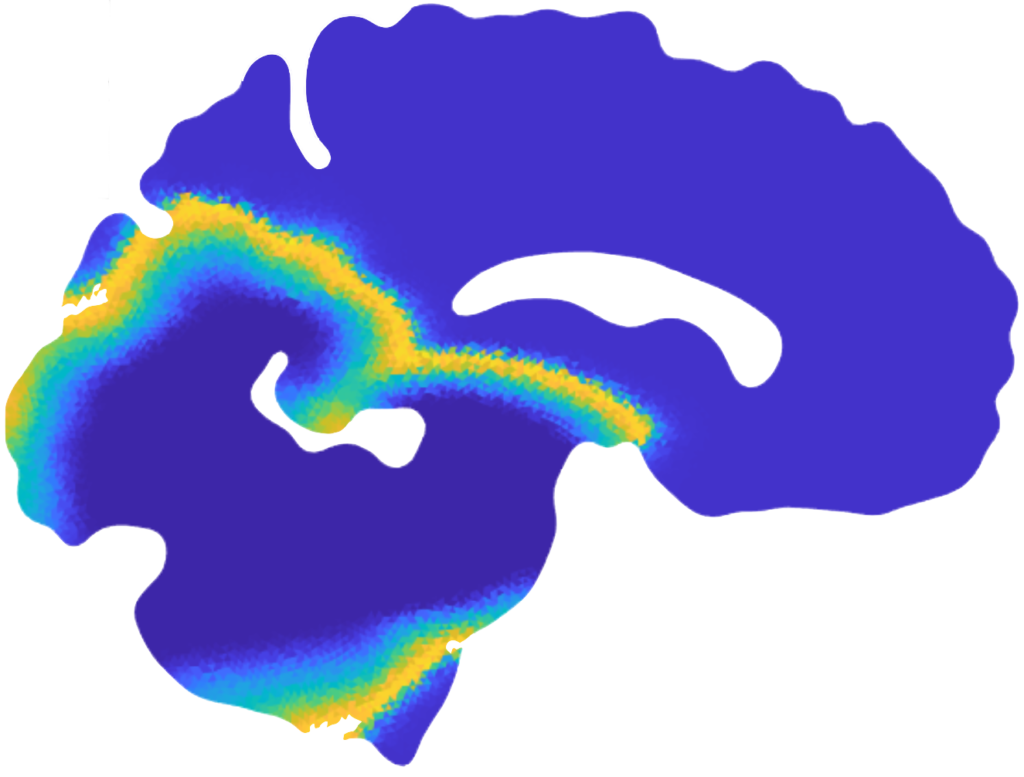
Mean value of the prions’ concentration inside some selected regions of the brain in Parkinson’s disease over 30 years (left) and position of brain regions (right) [Corti et al. (2023)].
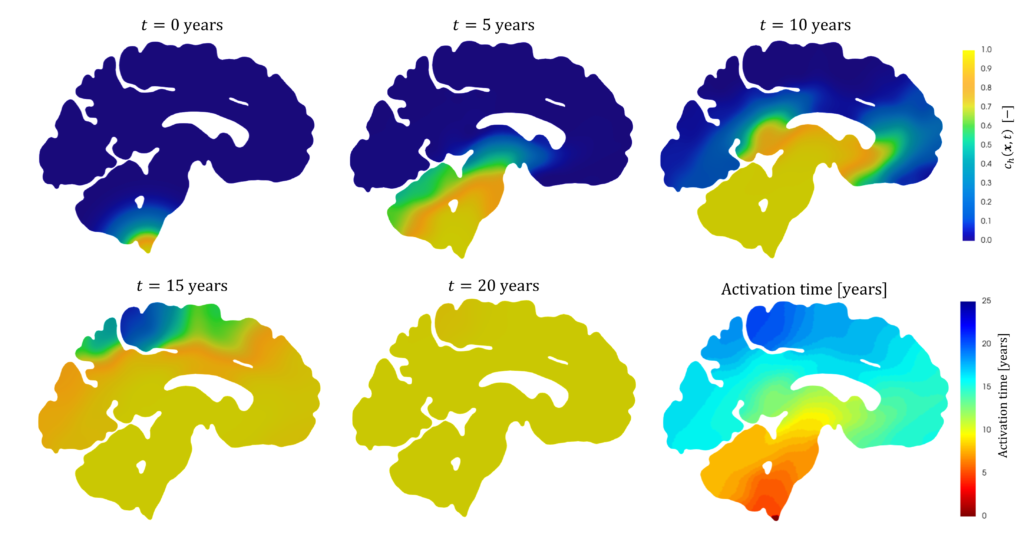
Patterns of α-synuclein concentration in Parkinson’s disease at different stages of the pathology and activation time of the pathology (bottom-right) [Corti et al. (2023)].
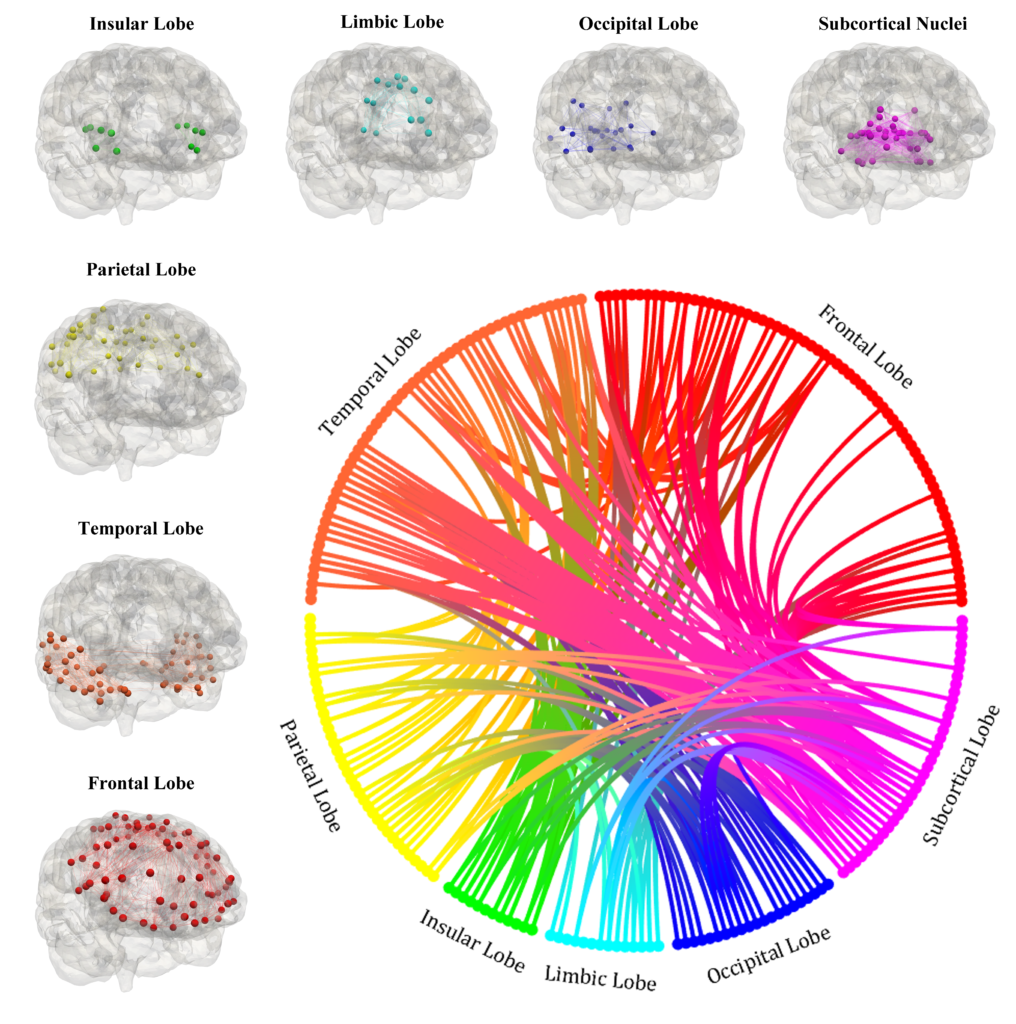
Local graphs of the seven regions of the brain and brain connectogram between different regions [Corti et al. (2023)].
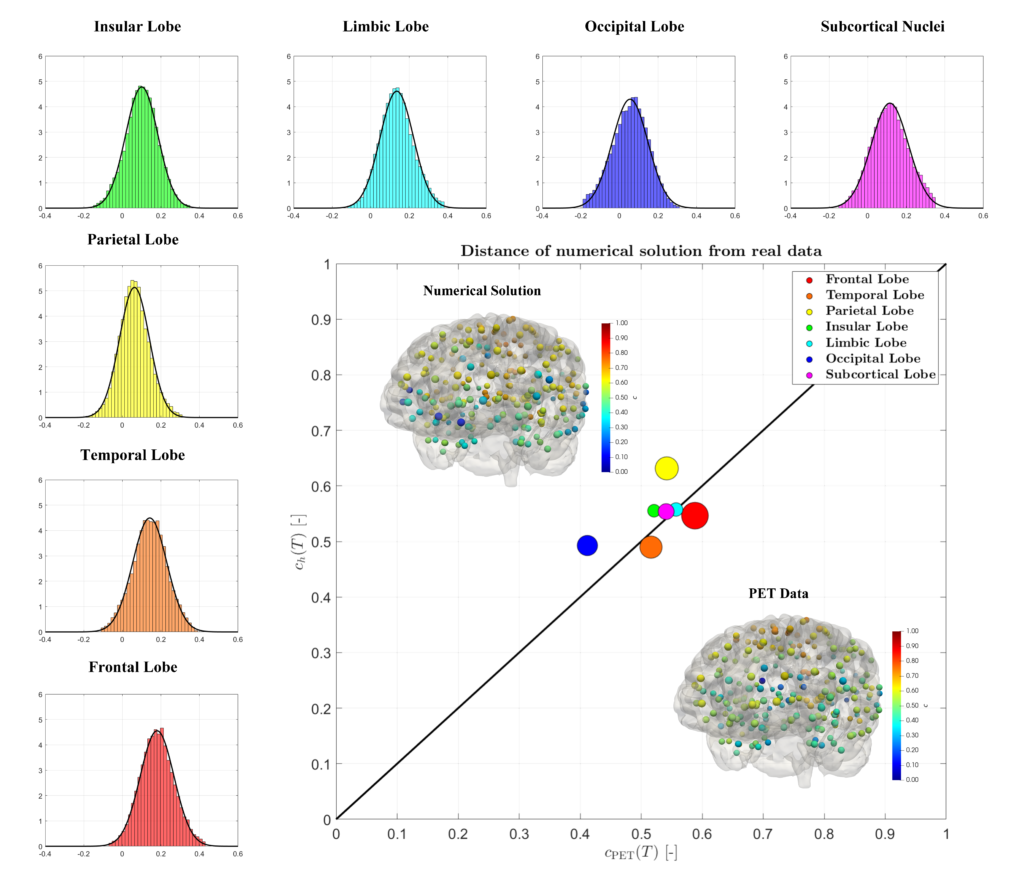
Histogram and Gaussian distribution associated with the reaction parameters of amyloid-β, in each lobe of the brain and comparison between the medical data and the numerical results for the concentration on a connectome [Corti et al. (2023)].
Neurological disorders
Numerical modelling of epileptic seizures. Epilepsy is a clinical neurological disorder characterized by recurrent and spontaneous seizures generating an abnormal high-frequency electrical activity of the brain. Despite several clinical studies that have permitted the development of specific pharmacological and surgical treatments to control the onset of seizures there is still an open debate on the mechanisms and optimal patient-specific treatment. We consider the bidomain model to mathematically describe seizure evolution in the grey and white matter, coupled with specific ionic models for neuronal modelling in which the different dynamics of the potential and ionic currents are considered. The mathematical model is discretized by means of discontinuous Galerkin methods. Suitable (space-time) adaptive schemes are proposed to exploit the flexibility of the numerical approach to better describe the sharp propagating fronts that characterize seizure propagation. The numerical results provide insights into the mechanisms underlying seizures and might, in the future, support precision medicine, thanks to methods capable of predicting patient-specific behaviour and suggesting optimal treatment.
This project is partially supported by
–Italian Research Center on High Performance Computing, Big Data and Quantum Computing (ICSC), under the NextGenerationEU project.
– PRIN 2020, research grant n. 20204LN5N5 “Advanced polyhedral discretisations of heterogeneous PDEs for multiphysics problems” funded by MUR (National Coordinator).